This writeup illustrates how almost anything can become a project if you read into it too much.

A few weeks ago, I was in the pub playing a very simple bingo game. The game works as follows:

• Each player recieves two random and unique playing cards from each suit to form a hand of eight cards
• A host sequentially draws cards from a randomly shuffled deck, announcing each card as it is drawn
• The first player to have all eight of their cards announced by the host wins

I was terrible at the pub quiz, so I decided to focus my mental efforts on two seemingly simple questions about the game, which eventually led to me getting ahead of myself:

• What’s the probability of having a “perfect” game. That is, a game where you win after the 8^th card is announced?

• In a game containing n players, how many cards are called out by the announcer before somone wins?

I thought I’d get my answer in under ten minutes but it took a little longer than that.

What’s the probability of having a “perfect” game?

My initial instinct was to try and simulate the “perfect game” scenario. I’m glad I resisted - it would’ve taken quite a bit of computation time to verify the probability. Luckily, there aren’t too many variables in this particular question. The chance of winning by the 8^th card call is unaffected by other players’ hands. Because of that it’s straightforward to construct an answer purely with combinatorics.

There are two cards per suit in a hand of eight cards. Using binomial coefficients, I calculated that there are 13 choose 2, or 78, combinations of cards when drawing two cards from a suit of 13 cards. Raise that to the power of the number of suits (i.e. 78⁴) to get the total possible combinations of a standard eight-card hand: 37015056 combinations. Only one of those combinations could achieve an 8-round win, which means that the probability of having a valid combination is 1 / 37015056 which, as a percentage, is 0.000002702 %.

That probability is an upper bound, though, because it assumes that the host’s randomly-shuffled deck conveniently contains two of each suit in its first eight cards. That isn’t always the case. Similar to hands, there’s 37015056 combinations of valid 8-card starters in a deck but there’s 52 choose 8, or 752538150, total starting combinations. Therefore, the probability of the host’s deck even has a valid starting combination is around 4.9 %.

Multiply the probability a host has a valid starter with the probability of somone actually having a winning combination to find that the overall probability of having a “perfect” game is around 1.32×10^-7 %.

How many card calls are there in an average game containing n players?

This is a little more complicated than the ‘ideal game’ scenario because there’s now a variable number of players to consider. Because of that, I developed a small console program with the following outer interface (link to source):

$ play-scottish-bingo number_of_players number_of_games [-s t]

Output:
winning_round_number, game 1
winning_round_number, game 2
.
.
.
winning_round_number, game [number_of_games]

Example:
$ play-scottish-bingo 5 3
35
37
33

In essence, it’s a very simple program that led me down the rabbit hole of shuffling methods, random seed generation, and proving shuffle correctness, with techniques such as comparing shuffles to derangement probabilities.

Once I got out of the rabbit hole, I used a shell script to run play-scottish-bingo with 0 to 100 players and measured the following results:

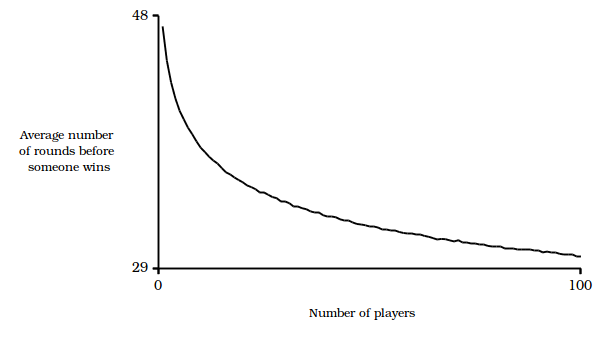
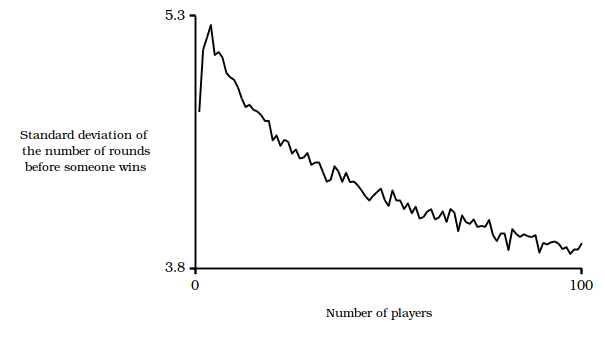
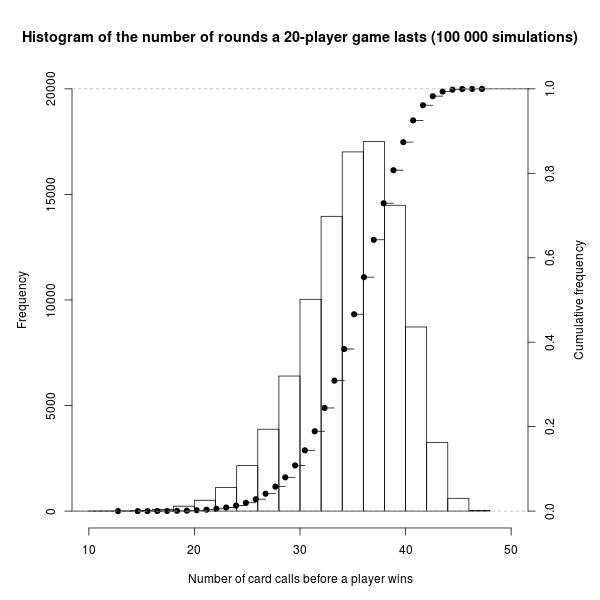
On the night I was playing, the pub contained around twenty patrons. For that scenario, the distribution looked as shown below. Based on those results, I’d expect the average game to be around 36 rounds long. A “rare” (<5 %) short game would last 26 rounds while a super rare (<0.5 %) short game would be 21 rounds long. A “rare” nail-biting long game would be around 41 rounds long with a super-rare long game being 44 rounds.

Psychologically speaking, shorter games tend to evoke an “is that it?” response from the crowd, it’s the longer games where anyone could win that are the most exciting. Most incarnations of this game usually ask players to call when seven of their eight cards have been called - an “I’m going to win” message. In longer games, many of the players will have made—and heard—that call and be waiting for their final card to be drawn - how intense!

Neverending Analysis

As I was doing this, I recoginzed that the analysis shown here is only the tip of the iceberg. What about different shuffling techniques? I assumed one-deck-per-player in this analysis. How does the distribution’s shape change with players and shuffles? I only took the averages of most datasets.

Then I looked at myself in the mirror and ended up at a scary conclusion:

I’m spending tens of hours analyzing, and coding simulators for, a simple card game. What am I? An undergraduate maths student?

After reaching that revelation, I stopped analyzing the bingo game. No more bingo games. For me, this is a hard lesson in “spending your time wisely”. I used to spend hundreds of hours trying to understand Blender’s texture nodes, many nights trying to redesign my University campus in Valve’s Hammer editor, and tens of hours creating vector art of common chemistry equipment. But this project, the bingo game, has finally opened my eyes. I’ll now only ever focus on important profitable and useful ideas.

My next project is a compiler that converts a high-level representation of an RS232 device into (C#, Python, etc.) libraries.

That one’s important.

Maybe.

No, not maybe. That idea’s definitely a winner.